Description
More about
Short list of features
More about
Technical Description
More about
Repositories and Download
More about
FLEUR is an all-electron density functional theory code based on the full-potential linearized augmented plane wave (FLAPW) method. A key difference with respect to the other MaX codes and indeed most other DFT codes lies in the treatment of all electrons on the same footing. The key component of FLEUR is a versatile DFT code for the ground-state properties of multicomponent one-, two- and three-dimensional solids. A special focus lies on non-collinear magnetism, the determination of exchange parameters, spin-orbit related properties (topological and Chern insulators, Rashba and Dresselhaus effect, magnetic anisotropies, Dzyaloshinskii-Moriya interaction) and magnon dispersion. A link to WANNIER90 enables the calculation of intrinsic and extrinsic transverse transport properties (anomalous-, spin- and inverse spin Hall effect, spin-orbit torque, anomalous Nernst effect, or topological transport properties such as the quantum spin-Hall effect etc.) in linear response theory using the Kubo formula. FLEUR includes LDA+U as well as hybrid-functionals for the accurate description of e.g. oxide materials and by linking against the libxc library, many more functionals are accessible. Using its link to the SPEX code more advanced treatments using the GW method or the GW+T approximation to magnetic excitations are possible starting from FLEUR. The well established FLAPW scheme is usually considered providing the most accurate DFT results and used as a reference for other methods. In addition, several quantities e.g. related to the properties of core-electrons are only available by the use of code not relying on the pseudopotential approximation.
Being applicable to all elements of the periodic table and by including all electrons, the code has its particular strength in the fields of electronically and magnetically complex materials, for example materials involving transition metals, heavy or rare-earth elements and thus is frequently used to calculate magnetic or spin-dependent properties in metals or complex oxide materials. It provides a natural link to other methods via the calculation of parameters for atomistic magnetic simulations or similar multiscale modelling methods.
- Diffusion
- Performance in HPC environments
Diffusion
FLEUR is distributed freely under the MIT license and has a growing user community. While about 3000 users registered on the older FLEUR-webpage the current free distribution scheme does no longer allow user tracking.
Performance in HPC environments
FLEUR is utilising several levels of parallelization to exploit both, intra-node and inter-node distribution of the calculation. On the most coarse level, the calculations can be split over different k-points (and q-points where present) leading to an excellent scaling behaviour. This can be seen in the following table in which we demonstrate excellent weak and good strong scalability on JUWELS booster up to roughly a quarter of the machine with a nominal performance of approximate 15 PFlops.
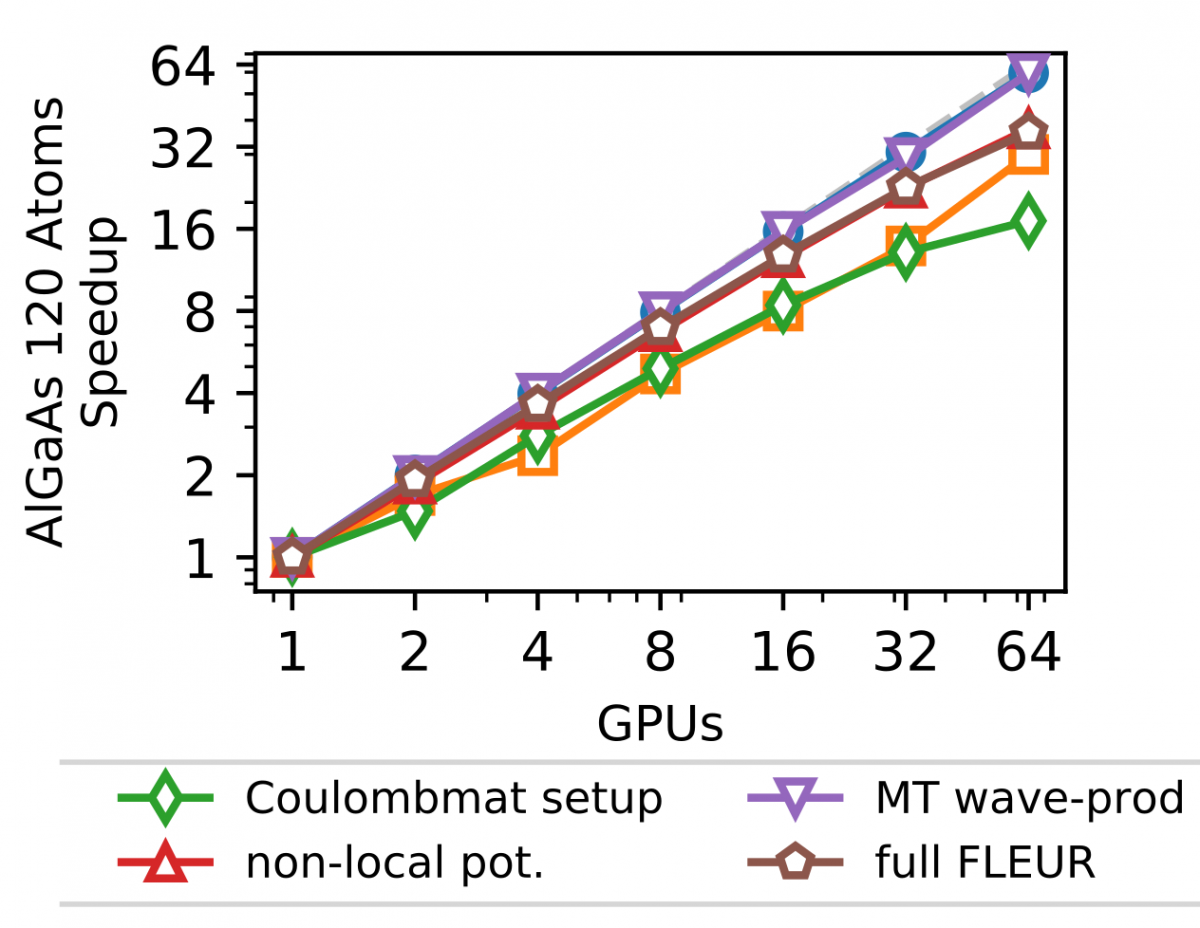
In addition to this outer parallelization level, FLEUR also employs more fine-grain parallelism, distributing the calculation associated with the different eigenstates. This parallelization is largely 'orthogonal' to the scaling shown before in which only a single GPU was assigned to this level. This level is strongly dependent on the details of the system as well as the kernel to be used. As an example (without any outer parallelization), we show in the Figure below the scalability for the calculation using hybrid functionals on the JURECA-DC cluster with 4 NVIDIA A100 cards per node, e.g. up to 16 nodes.
FLEUR is a feature-full, freely available FLAPW (full-potential linearized augmented planewave) code, based on density-functional theory. The FLAPW-method is an all-electron approach within density functional theory that is universally applicable to all atoms of the periodic table and to systems with compact as well as open structures. It is widely considered to be the most precise electronic structure method in solid state physics.
Among other things, FLEUR allows to calculate:
- Structural and magnetic ground state properties.
- Electronic properties like bandstructures, densities of states, etc.
- Charge densities, field gradients, or hyperfine fields.
- Magnetic interaction parameters used in discrete models.
- Input for GW-calculations, calculations of longitudinal and perpendicular electron transport.
Although FLEUR calculations can be performed for all kinds of materials, it is especially suited for:
- Magnetic systems (collinear or non-collinear) including spin-orbit coupling effects.
- Open systems (surfaces, wires, nanostructures).
- Transition metals, lanthanides, actinides.
Software
The FLEUR code family is a program package for calculating ground-state as well as excited-state properties of solids. It is based on the full-potential linearized augmented-plane-wave (FLAPW) method. The strength of the FLEUR code lies in applications to bulk, semi-infinite, two- and one-dimensional solids, solids of all chemical elements of the periodic table, solids with complex open structures, low symmetry, with complex non-collinear magnetism in combination with spin-orbit interaction, external electric fields, and the treatment of spin-dependent transport properties. It is an all-electron method and thus treats core and valence electrons and can deal with hyperfine properties. The inclusion of local orbitals allows a systematic extension of the LAPW basis that enables a precise treatment of semicore states, unoccupied states. A large variety of local and semi-local (GGA) exchange and correlation functionals are implemented, including the LDA+U approach.
Particular Libraries
FLEUR is an open source code distributed under the MIT Licence. The code source can be downloaded from its homepage or from a Gitlab service. FLEUR requires a Fortran and C compiler and as a minimum an BLAS/LAPACK and XML2 library. The code will massively benefit from highly optimized versions of the linear algebra libraries. In addition, the code can use libraries like MPI, SCALAPACK, HDF5, LibXC, ELPA, Elemental, Magma for parallel calculations, structured IO or for advanced functionality.
Parallel programming
Different parallelization paradigms are currently implemented in FLEUR, a shared memory OpenMP parallelism and a distributed memory MPI parallelism. The most basic and most efficient parallelisation distributed the different k-point over MPI. This leads to close to perfect scalability and load-balancing. The second and third level of parallelism consists of an additional MPI distribution of the remaining task, especially of the eigenvalue problem and an OpenMP parallelization which enables the efficient use on multi-core nodes. For larger systems these levels of parallelism are more important as the number of k-points will decrease and the memory requirements for a single k-point will increase.
I/O requirements
During a typical self-consistency cycle the code will only do limited IO. First the XML input and the initial charge density are read in and the final charge densities and the log/output file are written. It is possible to write also intermediate charge densities which might be advisable for larger simulations to allow restarts.


