Description
More about
Short list of features
More about
Technical Description
More about
Repositories and Download
More about
SIESTA is a pseudopotential-based density functional theory software whose strength lies in its use of atomic-like strictly-localised basis sets: the use of a "good first approximation" to the full problem decreases the number of basis functions needed to achieve a given accuracy, and the finite support of the orbitals leads to sparsity in the Hamiltonian and overlap matrices, thus enabling the use of
reduced-scaling methods. The functionalities of SIESTA include, amongst others, the calculation of energies and forces, molecular-dynamics simulations, band structures, densities of states, spin-orbit couplings, van der Waals functionals, hybrid functionals, DFT+U for correlated systems, real-time TDDFT, and density-functional perturbation theory. SIESTA contains the transport code TranSIESTA, which is based on the non-equilibrium Green function formalism and enables open-boundary condition calculations by extending periodic regions with bulk electrodes. TranSIESTA's features include advanced inversion algorithms, multiple electrodes, thermo-electric calculations, real-space calculations (without k-points), and phonon transport calculations. SIESTA can also be used to provide base calculations for the execution of other electronic structure packages such as BerkeleyGW (optical properties and quasiparticle excitations), Gollum (transport), Wannier90 (maximally localized Wannier functions and advanced electronic properties), or i-PI (nuclear quantum effects in condensed phase systems).
SIESTA is known to be used in a wide range of applications, encompassing materials science, nanotechnology, catalysis, biological sciences (including interaction between organic and inorganic materials), geology and materials under high pressure, Martian geochemistry, materials for nuclear reactors, and astrophysical and atmospheric systems.
Diffusion
SIESTA is an open-source software distributed for free under a GPL license. Release tarballs and development versions can be downloaded from its GitLab repository, while tutorials and other learning materials are publicly accessible from a dedicated documentation site. Further hands-on training activities are organised routinely, and SIESTA developers (about 20 of them active at the moment) can be easily reached through the SIESTA mailing list and the usual forums of the electronic structure community. SIESTA has a large use base, as displayed by the number of citations that the reference publication [1] receives every year, well over 600 (more than 12,000 citations by early 2022).
Performance in HPC environments
SIESTA is written in modern Fortran with both MPI and OpenMP parallelism. For most problems, the most computationally-demanding stage of SIESTA execution is the solver stage (calculation of energy eigenvalues from the above-mentioned sparse objects). On the one hand, SIESTA provides a range of solvers of its own, from cubic-scaling diagonalisation to linear-scaling methods,
that exploit existing linear algebra libraries such as ScaLAPACK, ELPA, and DBCSR.
On the other hand, SIESTA can leverage a number of libraries that implement favourably-scaling solvers, such as Chess (Fermi Operator Expansion method) and PEXSI (Pole EXpansion and Selected Inversion method). All these libraries are designed for parallel execution, and they are progressively incorporating support for offloading to an increasing breadth of GPU architectures.
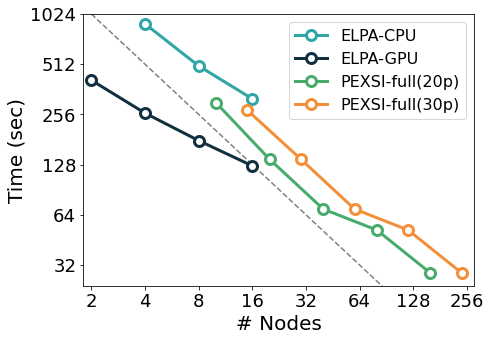
The figure below exemplifies the scaling of some of the solvers mentioned above in the Marconi 100 supercomputer: starting from the CPU version of the ELPA solver, the same solver with GPU offloading displays a significant speed-up, although with some degradation in its scaling probably due to no longer saturating the GPUs. In comparison, the (CPU-only) PEXSI solver allows for scaling to a significantly larger number of nodes with less degradation. The accuracy of the PEXSI solver improves with the number of poles used in the expansion it performs; it can be seen how the increased accuracy enables scaling to a larger number of nodes, thus not increasing the time to solution.
References
-
[1] J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon, and D. Sanchez-Portal, The SIESTA method for ab initio order-n materials simulation, J. Phys.: Condens. Matter 14, 2745 (2002).
SIESTA is a first-principles materials simulation code based on density-functional theory (DFT). It uses atomic orbitals with finite support as a basis set, allowing unlimited multiple-zeta and angular momenta, polarization and off-site orbitals. Apart from the increased efficiency brought by the reduced cardinality of an atomic-orbital basis set, finite-support basis orbitals are the key for calculating the (sparse) Hamiltonian and overlap matrices in O(N) operations, and for the use of reduced-scaling algorithms. SIESTA uses the standard Kohn-Sham self-consistent density functional method in the local density (LDA-LSD) or generalized gradient (GGA) approximations, and also implements functionals capable of describing van der Waals interactions. It employs norm-conserving pseudopotentials in their fully nonlocal (Kleinman-Bylander) form. SIESTA uses a real-space grid in order to calculate the Hartree and exchange-correlation potentials and their matrix elements.
The SIESTA package includes a TranSiesta module to enable electronic-transport calculations within the non-equilibrium Green’s functions formalism.
SIESTA can provide:
- Total energies, forces, and stress.
- Band structures.
- Local and orbital-projected density of states.
- Electron density.
- Spin polarized calculations (collinear or not, including spin-orbit coupling).
- k-sampling of the Brillouin zone.
- COOP and COHP curves for chemical bonding analysis.
- Dielectric polarization (Berry phase method).
- Atomic, orbital and bond populations (Mulliken).
- Geometry relaxation, fixed or variable cell.
- Constant-temperature molecular dynamics (Nose thermostat).
- Variable cell dynamics (Parrinello-Rahman).
- Vibrations (phonons), in both the frozen-phonon and linear-response modes.
- Time-dependent density-functional-theory.
- Electronic-transport within the non-equilibrium Green’s function formalism.
Software
SIESTA is a Fortran code to perform materials simulations within DFT. Two main phases can be distinguished in a typical electronic-structure calculation: the setup of the Hamiltonian, which scales as O(N) with the size of the system, and deals mostly with sparse data structures, and the solving of the electronic structure, whose scaling can range from linear to cubic, depending on the algorithm. Parallelization of the ‘setup’ phase is mainly done with MPI, with some sections also parallelized with OpenMP. Data distribution is done over orbitals and over grid points. The solver stage is typically the most time consuming for large systems. The default solver, and the most efficient for moderately-sized systems, is based on diagonalization, with an initial conversion of the sparse matrices to dense form. Other solvers (i.e., PEXSI, CheSS) deal directly with the sparse matrices and have thus a smaller memory footprint. For massively parallel execution, the PEXSI solver offers various levels of parallelization and is able to scale to tens of thousands of processes, showing also a reduced complexity scaling, which can reach O(N) for quasi-one-dimensional systems. The TranSIESTA module uses advanced algorithms and incorporates a nearly complete dual MPI/OpenMP parallelization.
Particular Libraries
SIESTA is an open source code distributed under the GNU General Public Licence. Development is currently hosted on the GitLab platform. SIESTA works with Fortran (and C for some functionality) and uses standard optimized libraries such as BLAS, LAPACK, ScaLAPACK, and netCDF/HDF5. Some optional functionality depends on domain-specific libraries such as ELSI, CheSS, libXC, and/or the embedding of a (lightweight) Lua interpreter together with associated glue libraries. Note that some of the functional modules within SIESTA are being made stand-alone and released as library packages within the Electronic Structure Library (ESL).
Parallel programming
As mentioned above, the main parallelization paradigm is MPI, with some modules (notably TranSIESTA) offering also parallelization using OpenMP. The solver stage, when using standard diagonalization algorithms, can also benefit from “library-mode” OpenMP.
I/O requirements
Checkpointing is based on the saving of the density matrix, which is a sparse data object in SIESTA, and hence moderate in size. Some modes of operation require the saving of (a subset of) the wavefunctions, which is a more substantial demand, but still manageable due to the low-cardinality of SIESTA’s basis set.


